双端 Diff 算法
双端比较原理
简单 Diff
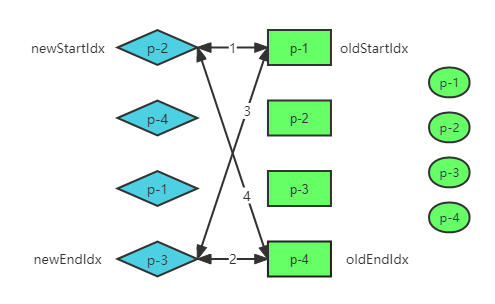
简单 Diff 算法的问题在于,它对 DOM 的移动操作并不是最优的。以下面这个子节点列表更新为例: 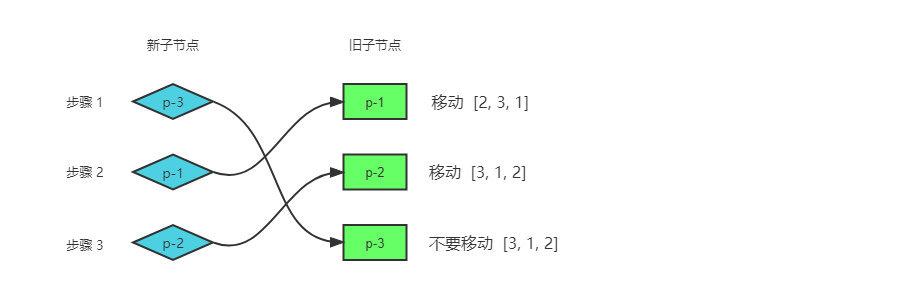
如图可见,使用简单 diff 算法在本次比较过程中需要两次 DOM 移动操作,分别是将 p-1 和 p-2 移动到 p-3 之后。
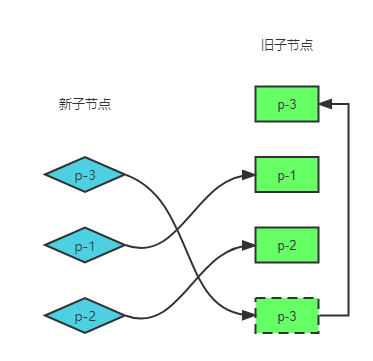
然而,上述更新过程并非最优解。实际上,我们只要一次 DOM 移动操作即可完成更新,即将真实 DOM 节点 p-3 移动到真实 DOM 节点 p-1 前面。
双端 Diff
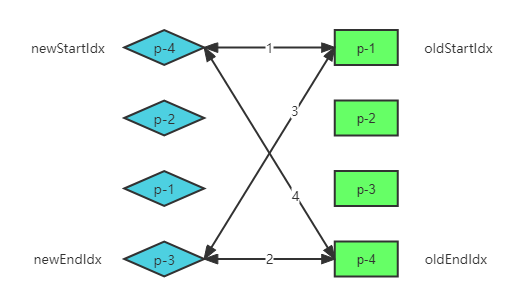
双端 Diff 算法,顾名思义就是使用四个指针,分别指向新旧子节点数组的头尾,然后按照一定的顺序从头尾向中间进行遍历处理:
- 路线 1 匹配,自增 newStartIdx 和 oldStartIdx
- 路线 2 匹配,自减 newEndIdx 和 oldEndIdx
- 路线 3 匹配,表示原本在头部的节点现在要移动到尾部,那么移动真实 DOM 的 oldStartIdx 对应节点到 oldEndIdx 节点之后
- 路线 4 匹配,表示原本在尾部的节点现在要移动到头部,那么移动真实 DOM 的 oldEndIdx 对应节点到 oldStartIdx 节点之前
function patchKeyedChildren(n1, n2, container) {
const oldChildren = n1.children
const newChildren = n2.children
let oldStartIdx = 0
let oldEndIdx = oldChildren.length - 1
let newStartIdx = 0
let newEndIdx = newChildren.length - 1
let oldStartVNode = oldChildren[oldStartIdx]
let oldEndVNode = oldChildren[oldEndIdx]
let newStartVNode = newChildren[newStartIdx]
let newEndVNode = newChildren[newEndIdx]
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
if (oldStartVNode.key === newStartVNode.key) {
patch(oldStartVNode, newStartVNode, container)
oldStartVNode = oldChildren[++oldStartIdx]
newStartVNode = newChildren[++newStartIdx]
} else if (oldEndVNode.key === newEndVNode.key) {
patch(oldEndVNode, newEndVNode, container)
oldEndVNode = oldChildren[--oldEndIdx]
newEndVNode = newChildren[--newEndIdx]
} else if (oldStartVNode.key === newEndVNode.key) {
patch(oldStartVNode, newEndVNode, container)
insert(oldStartVNode.el, container, newEndVNode.el.nextSibling)
oldStartVNode = oldChildren[++oldStartIdx]
newEndVNode = newChildren[--newEndIdx]
} else if (oldEndVNode.key === newStartVNode.key) {
patch(oldEndVNode, newStartVNode, container)
insert(oldEndVNode.el, container, oldStartVNode.el)
oldEndVNode = oldChildren[--oldEndIdx]
newStartVNode = newChildren[++newStartIdx]
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
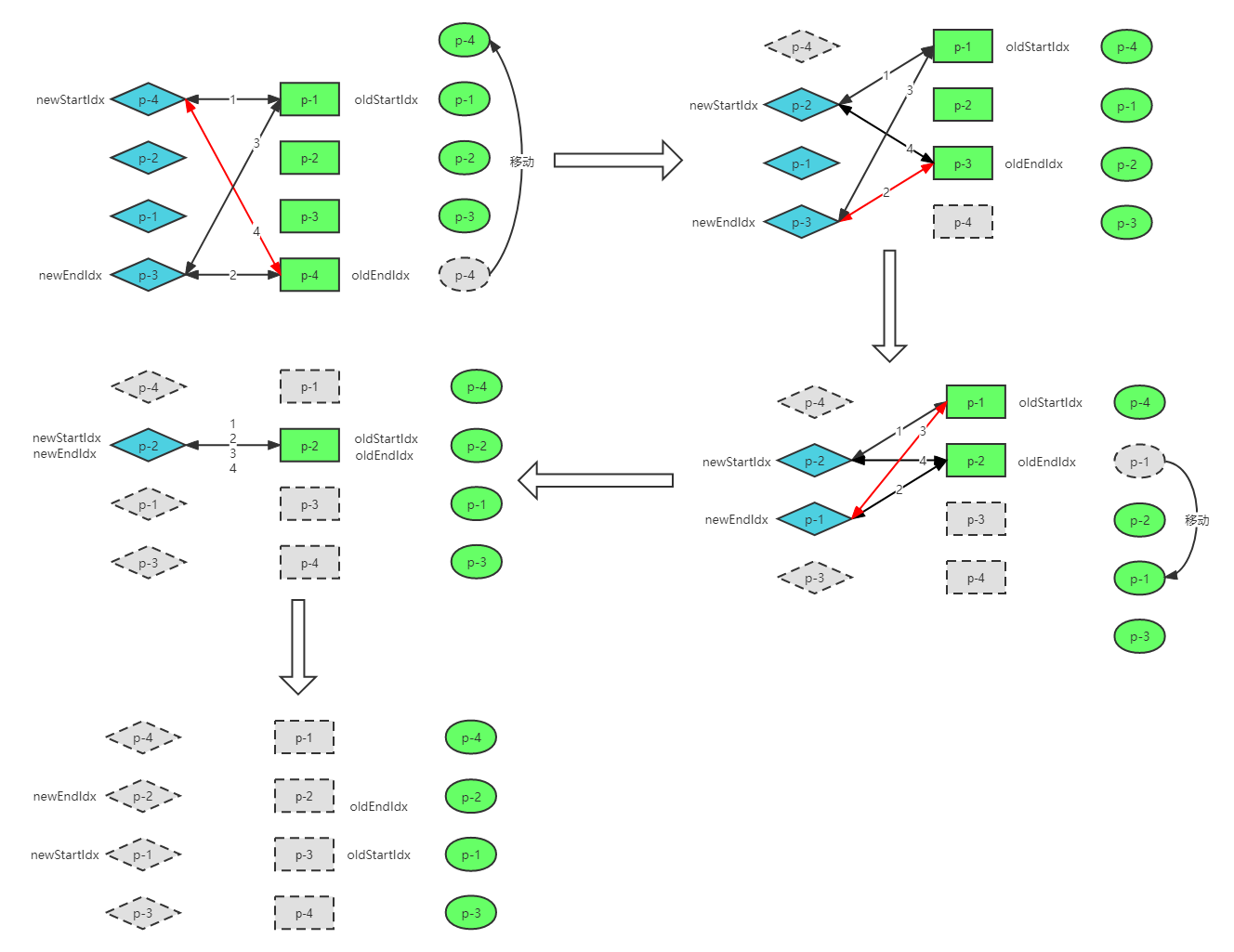
此时,真实 DOM 节点的顺序与新的一组子节点的顺序相同了:p-4、p-2、p-1、p-3。
另外,在这一轮更新完成之后,所有 newStartIdx 和所有 oldStartIdx 的值都小于 newEndIdx 和 oldEndIdx。循环终止,双端 Diff 执行完毕。
双端比较的优势
经过分析双端 Diff 算法,现在我们只需要一次 DOM 移动操作,而之前的简单 Diff 算法需要两次移动操作。

非理性状况的处理方式
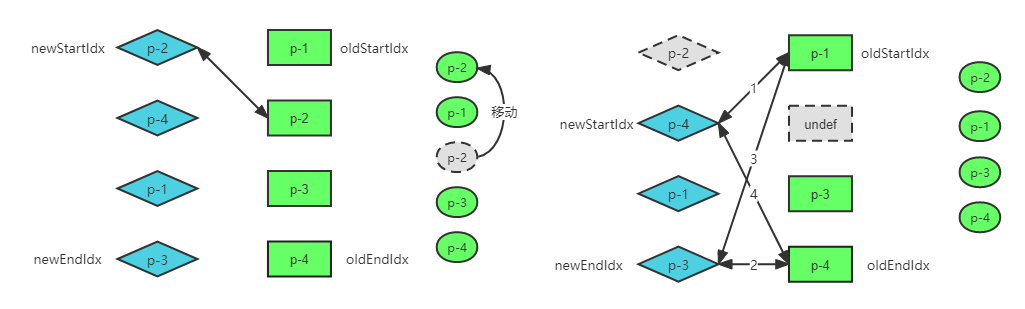
在之前的例子当中,我们使用的是比较理性的例子。Diff 过程中总会命中四个步骤中的一个,这是非常理想的情况。但实际上,并非所有情况都这么理想:
使用目前的双端 Diff 算法进行处理,会发现无法命中四个步骤的任何一步。针对这种情况,我们只能增加额外的步骤来处理这种情况
🚀 具体的做法是,拿新的一组子节点中的头部节点去旧的一组子节点中寻找。如果找到了可复用的旧节点,把这个节点移动到头部,并把这个旧节点标记为 undefined,后续执行如果遇到 undefined 旧节点直接跳过即可。
代码需要新增一个分支来处理为命中的情况,另外需要跳过旧子节点为 undefined 的情况:
function patchKeyedChildren(n1, n2, container) {
// ...
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
// 如果旧节点为 undefined,跳过
if (!oldStartVNode) {
oldStartVNode = oldChildren[++oldStartIdx]
} else if (!oldEndVNode) {
oldEndVNode = newChildren[--oldEndIdx]
} else if (oldStartVNode.key === newStartVNode.key) {
patch(oldStartVNode, newStartVNode, container)
oldStartVNode = oldChildren[++oldStartIdx]
newStartVNode = newChildren[++newStartIdx]
} else if (oldEndVNode.key === newEndVNode.key) {
patch(oldEndVNode, newEndVNode, container)
oldEndVNode = oldChildren[--oldEndIdx]
newEndVNode = newChildren[--newEndIdx]
} else if (oldStartVNode.key === newEndVNode.key) {
patch(oldStartVNode, newEndVNode, container)
insert(oldStartVNode.el, container, newEndVNode.el.nextSibling)
oldStartVNode = oldChildren[++oldStartIdx]
newEndVNode = newChildren[--newEndIdx]
} else if (oldEndVNode.key === newStartVNode.key) {
patch(oldEndVNode, newStartVNode, container)
insert(oldEndVNode.el, container, oldStartVNode.el)
oldEndVNode = oldChildren[--oldEndIdx]
newStartVNode = newChildren[++newStartIdx]
} else {
// 遍历旧 children,试图寻找与 newStartVNode 拥有相同 key 值的元素
const idxInOld = oldChildren.findIndex(
node => node.key === newStartVNode.key
)
// 移动该节点到子节点头部,并标记为 undefined
if (idxInOld > 0) {
const vnodeToMove = oldChildren[idxInOld]
patch(vnodeToMove, newStartVNode, container)
insert(vnodeToMove.el, container, oldStartVNode.el)
oldChildren[idxInOld] = undefined
newStartVNode = newChildren[++newStartIdx]
}
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
最后,对于目前的这个例子,后续的处理步骤如下:
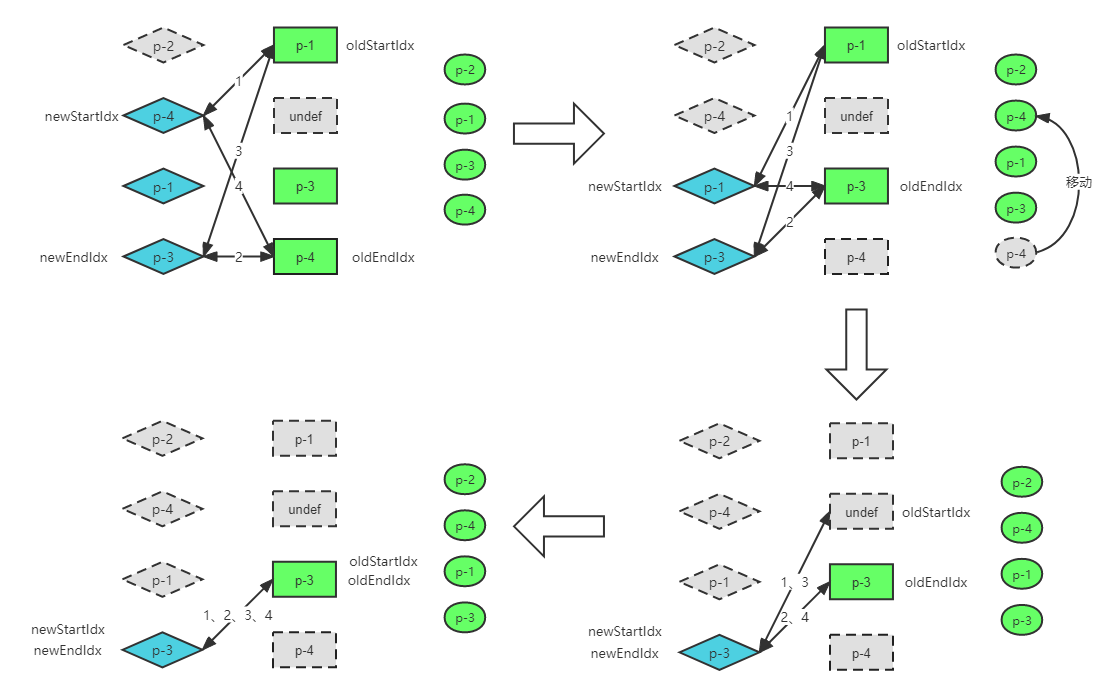
添加新元素
一轮未匹配
在之前的处理中,如果在一轮比较中,代码不会命中四个步骤的任何一步。这时,我们会拿新子节点的第一个节点去旧子节点列表中寻找可复用节点,然而并非总是能找到:p-4、p-1、p-3、p-2
首先,我们尝试一轮比较,发现在四个步骤的比较中都找不打可复用的节点。于是我们尝试拿新的一组子节点的第一个节点 p-4 去旧的一组子节点当中寻找可复用节点,但是在旧的一组子节点当中并没有匹配到 key 相同的节点。
🚀 说明这个节点是新子节点,并且是新子节点的头部节点,我们只需要把这个节点挂载到当前的头部节点即可。
遍历被遗漏
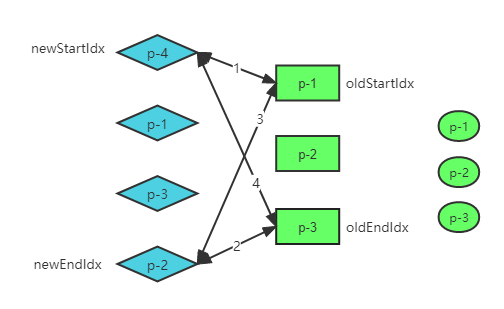
除了在一轮比较当中未匹配步骤的情况,我们更改之前的例子为:p-4、p-1、p-2、p-3
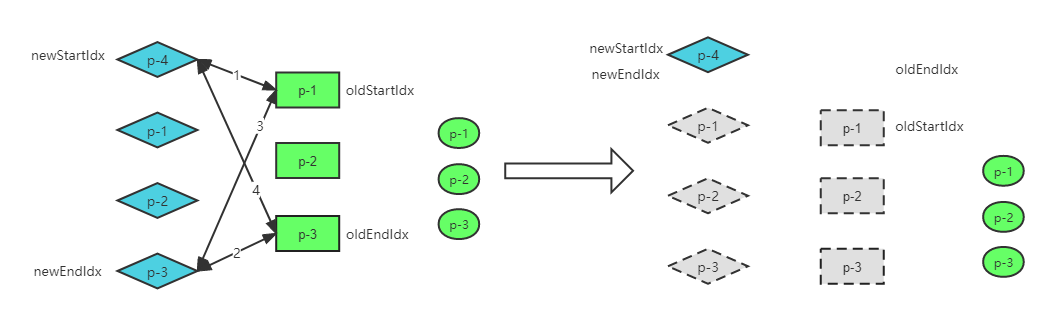
当双端 Diff 多轮处理完毕之后,剩下了一个 p-4节点,这个节点在整个更新过程中被遗漏了,没有得到任何处理,说明目前的算法还有缺陷需要额外处理。
🚀 遗漏的新子节点都是要新增的新子节点,按序遍历挂载到头部即可。
const idxInOld = oldChildren.findIndex(
node => node.key === newStartVNode.key
)
if (idxInOld > 0) {
const vnodeToMove = oldChildren[idxInOld]
patch(vnodeToMove, newStartVNode, container)
insert(vnodeToMove.el, container, oldStartVNode.el)
oldChildren[idxInOld] = undefined
} else {
// 如果未找到可复用节点,将当前节点挂载在头部即可
patch(null, newStartVNode, container, oldStartVNode.el)
}
newStartVNode = newChildren[++newStartIdx]
2
3
4
5
6
7
8
9
10
11
12
13
14
if (oldEndIdx < oldStartIdx && newStartIdx <= newEndIdx) {
// 如果新子节点列表有处理遗漏的节点,则添加
for (let i = newStartIdx; i <= newEndIdx; i++) {
patch(null, newChildren[i], container, oldStartVNode.el)
}
}
2
3
4
5
6
function patchKeyedChildren(n1, n2, container) {
const oldChildren = n1.children
const newChildren = n2.children
let oldStartIdx = 0
let oldEndIdx = oldChildren.length - 1
let newStartIdx = 0
let newEndIdx = newChildren.length - 1
let oldStartVNode = oldChildren[oldStartIdx]
let oldEndVNode = oldChildren[oldEndIdx]
let newStartVNode = newChildren[newStartIdx]
let newEndVNode = newChildren[newEndIdx]
while (oldStartIdx <= oldEndIdx && newStartIdx <= newEndIdx) {
if (!oldStartVNode) {
oldStartVNode = oldChildren[++oldStartIdx]
} else if (!oldEndVNode) {
oldEndVNode = newChildren[--oldEndIdx]
} else if (oldStartVNode.key === newStartVNode.key) {
patch(oldStartVNode, newStartVNode, container)
oldStartVNode = oldChildren[++oldStartIdx]
newStartVNode = newChildren[++newStartIdx]
} else if (oldEndVNode.key === newEndVNode.key) {
patch(oldEndVNode, newEndVNode, container)
oldEndVNode = oldChildren[--oldEndIdx]
newEndVNode = newChildren[--newEndIdx]
} else if (oldStartVNode.key === newEndVNode.key) {
patch(oldStartVNode, newEndVNode, container)
insert(oldStartVNode.el, container, oldEndVNode.el.nextSibling)
oldStartVNode = oldChildren[++oldStartIdx]
newEndVNode = newChildren[--newEndIdx]
} else if (oldEndVNode.key === newStartVNode.key) {
patch(oldEndVNode, newStartVNode, container)
insert(oldEndVNode.el, container, oldStartVNode.el)
oldEndVNode = oldChildren[--oldEndIdx]
newStartVNode = newChildren[++newStartIdx]
} else {
const idxInOld = oldChildren.findIndex(
node => node.key === newStartVNode.key
)
if (idxInOld > 0) {
// 找到可复用的头部节点,patch & 移动到头部
const vnodeToMove = oldChildren[idxInOld]
patch(vnodeToMove, newStartVNode, container)
insert(vnodeToMove.el, container, oldStartVNode.el)
oldChildren[idxInOld] = undefined
} else {
// 如果未找到可复用节点,将当前节点挂载在头部即可
patch(null, newStartVNode, container, oldStartVNode.el)
}
newStartVNode = newChildren[++newStartIdx]
}
}
if (oldEndIdx < oldStartIdx && newStartIdx <= newEndIdx) {
// 如果新子节点列表有处理遗漏的节点,则添加
for (let i = newStartIdx; i <= newEndIdx; i++) {
patch(null, newChildren[i], container, oldStartVNode.el)
}
} else if (newEndIdx < newStartIdx && oldStartIdx <= oldEndIdx) {
// 如果旧子节点列表有处理遗漏的节点,则卸载
for (let i = oldStartIdx; i <= oldEndIdx; i++) {
unmount(oldChildren[i])
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
移除不存在的元素
在双端 Diff 处理过程中,未被复用的旧子节点就是需要卸载的节点。
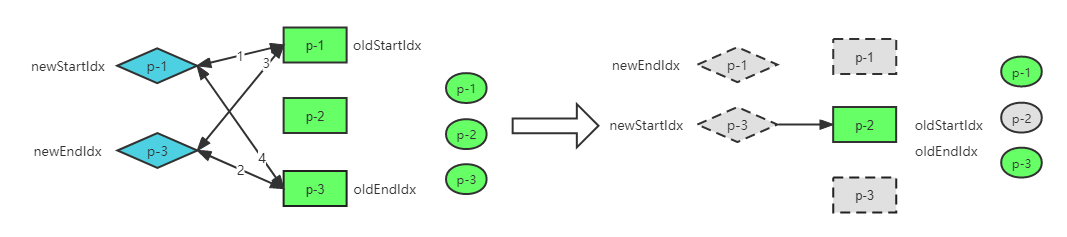
🚀 如上图所示,当 diff 多轮处理完毕之后,p-2 这个节点处在 [oldStartIdx, oldEndIdx] 区间内,说明这个节点未被复用到,应该被卸载。
if (oldEndIdx < oldStartIdx && newStartIdx <= newEndIdx) {
// 添加新节点
for (let i = newStartIdx; i <= newEndIdx; i++) {
patch(null, newChildren[i], container, oldStartVNode.el)
}
} else if (newEndIdx < newStartIdx && oldStartIdx <= oldEndIdx) {
// 移除旧节点
for (let i = oldStartIdx; i <= oldEndIdx; i++) {
unmount(oldChildren[i])
}
}
2
3
4
5
6
7
8
9
10
11
总结
双端 Diff 指的是,在新旧两组子节点的四个端点之间分别进行比较,并试图找到可以复用的节点。相比简单 Diff 算法,双端 Diff 算法的优势在于,对于同样的更新场景,执行的 DOM 移动操作次数更少。