JavaScript数据结构和算法

栈

栈是一种遵从后进先出(LIFO)原则的有序集合，新添加或待删除的元素都保存在栈的同一端，称之为栈顶，另一端叫栈底。

class Stack {
  constructor () {
    this.count = 0
    this.items = {}
  }
  push (element) {
    this.items[this.count] = element
    this.count++
  }
  size () {
    return this.count
  }
  isEmpty () {
    return this.size() === 0
  }
  pop () {
    if (this.isEmpty()) {
      return undefined
    }
    this.count--
    const result = this.items[this.count]
    delete this.items[this.count]
    return result
  }
  peek () {
    return this.items[this.count - 1]
  }
  clear () {
    this.count = 0
    this.items = {}
  }
  toString () {
    if (this.isEmpty()) {
      return ''
    }
    let str = this.items['0']
    for(let i = 1; i < this.count; i++) {
      str = `${str},${this.items[i]}`
    }
    return str
  }
}

队列和双端队列

队列

队列是一种遵循先进先出(FIFO)原则的一组有序的项，队列在尾部添加新元素，并从顶部移除元素，而双端队列是一种将栈的原则和队列的原则混合在一起的数据结构。

class Queue {
  constructor () {
    this.count = 0
    this.lowestCount = 0
    this.items = {}
  }
  size () {
    return this.count - this.lowestCount
  }
  isEmpty () {
    return this.size() === 0
  }
  enqueue (element) {
    this.items[this.count] = element
    this.count++
  }
  dequeue () {
    if (this.isEmpty()) {
      return undefined
    }
    const result = this.items[this.lowestCount]
    delete this.items[this.lowestCount]
    this.lowestCount++
    return result
  }
  peek () {
    if (this.isEmpty()) {
      return undefined
    }
    return this.items[this.lowestCount]
  }
  clear () {
    this.count = 0
    this.lowestCount = 0
    this.items = {}
  }
  toString () {
    if (this.isEmpty()) {
      return ''
    }
    let objStr = this.items[this.lowestCount]
    for(let i = this.lowestCount + 1; i < this.count; i++) {
      objStr = `${objStr},${this.items[i]}`
    }
    return objStr
  }
}

代码测试队列：

const queue = new Queue()
console.log(queue.isEmpty())  // true
queue.enqueue('AAA')
queue.enqueue('BBB')
queue.enqueue('CCC')
console.log(queue.isEmpty())  // false
console.log(queue.size())     // 3
console.log(queue.toString()) // AAA,BBB,CCC
console.log(queue.peek())     // AAA
queue.dequeue()
queue.clear()
console.log(queue.isEmpty())  // true

双端队列

双端队列是一种允许我们同时从前端和后端添加和移除元素的特殊队列，在计算机科学中，双端队列的一个常见应用是存储一系列撤销操作，每当用户在软件中进行了一个操作，该操作被存在一个双端队列中，当用户点击撤销按钮时，该操作会被从双端队列中弹出，表示它被从后面移除了。在进行预先定义的一定数量的操作后，最新进行的操作会被从双端队列的前端移除。

class Deque {
    constructor() {
        this.count = 0;
        this.lowestCount = 0;
        this.items = {};
    }
    addBack(element) {
        this.items[this.count] = element;
        this.count++;
    }
    addFront(element) {
        if (this.isEmpty()) {
            this.addBack(element);
        } else if (this.lowestCount > 0) {
            this.lowestCount--;
            this.items[this.lowestCount] = element;
        } else {
            // lowestCount = 0,全部后移一步
            for (let i = this.count; i > 0; i--) {
                this.items[i] = this.items[i -1];
            }
            this.count++;
            this.lowestCount = 0;
            this.items[0] = element;
        }
    }
    removeFront() {
        if (this.isEmpty()) {
            return undefined;
        }
        const result = this.items[this.lowestCount];
        delete this.items[this.lowestCount];
        this.lowestCount++;
        return result;
    }
    peekFront() {
        if (this.isEmpty()) {
            return undefined;
        }
        return this.items[this.lowestCount];
    }
    isEmpty() {
        return this.count - this.lowestCount === 0;
    }
    size() {
        return this.count - this.lowestCount;
    }
}

链表

链表

在大多数语言中数组的大小是固定的，在数组的起点或者中间插入或移除项的成本很高。而链表的出现解决了这个问题

链表存储有序的元素集合，但不同于数组，链表中的元素在内存中并不是连续放置的。每个与元素由一个存储自身的节点和一个指向下一个元素的引用组成，所以链表的一个好处在于：添加和移除元素的时候不需要移动其它元素。

然而，链表需要使用指针，因此不像在数组中可以直接访问任何位置的任何元素，链表需要我们从起点或者头开始迭代链表直到找到所需的元素。

class Node {
  constructor (element) {
    this.element = element
    this.next = null
  }
}

双向链表

双向链表和普通链表的区别在于：在链表中，一个节点只有链向下一个节点的链接，而在双向链表中，链表是双向的，一个链向下一个元素，另一个链向前一个元素。

class DoublyNode extends Node {
  constructor (element, next, prev) {
    super(element, next)
    this.prev = prev
  }
} 

循环链表

循环链表可以像普通(单向)链表一样只有单向引用，也可以像双向链表一样有双向引用。

循环链表和普通(单向)链表的唯一区别在于：最后一个元素的指针不是null或者undefined，而是指向第一个元素head。

集合Set

class Set {
  constructor () {
    this.items = {}
  }
  has (element) {
    return element in this.items
  }
  add (element) {
    if (!this.has(element)) {
      this.items[element] = element
      return true
    }
    return false
  }
  delete (element) {
    if (this.has(element)) {
      delete this.items[element]
      return true
    }
    return false
  }
  clear () {
    this.items = {}
  }
  size () {
    return Object.keys(this.items).length
  }
  values () {
    return Object.values(this.items)
  }
}

字典和散列表

字典

概念

在字典Dictionary（或映射Map）中，我们用[键，值]对的形式来存储数据。

在散列表中也是一样（也是以[键，值]对的形式来存储数据）。

但是两种数据结构的实现方式略有不同，例如字典中的每个键只能有一个值

字典也称映射、符号表或关联数组。在计算机科学中，字典经常用来保存对象的引用地址

散列表HashTable

散列表也叫HashTable类或者HashMap类，它是Dictionary类的一种散列实现方式。

散列算法：散列算法的作用是尽可能的快的在数据结构中找到一个值，因为它是字典的一种实现，所以可以用作关联数组，它也可以用来对数据库进行索引。当我们使用关系型数据库的时候，创建一个新的表时，一个不错的做法是同时创建一个索引来更快的查询到记录的key，在这种情况下，散列表可以用来保存键和对表中记录的引用。

散列表的创建需要一个hash函数生成键，即散列函数

loseloseHashCode(key) {
  if (typeof key === 'number') {
    return key;
  }
  const tableKey = this.toStrFn(key);
  let hash = 0;
  for (let i = 0; i < tableKey.length; i++) {
    hash += tableKey.charCodeAt(i);
  }
  return hash % 37;
}

hashCode(key) {
  return this.loseloseHashCode(key);
}

// 更好的散列函数可以降低冲突
djb2HashCode(key) {
  const tableKey = this.toStrFn(key);
  let hash = 5381;
  for (let i = 0; i < tableKey.length; i++) {
    hash = (hash * 33) + tableKey.charCodeAt(i);
  }
  return hash % 1013;
}

有时候，一些键会有相同的散列值。不同的值在散列表中对应相同位置的时候，我们称其为冲突。

处理冲突有几种方法：

• 分离链接：包括为散列表的每一个位置创建一个链表并将元素存储在里面。它是解决冲突的最简单的方法，但是在HashTable实例之外还需要额外的存储空间

• 线性探查：将元素直接存储到表中，而不是在单独的数据结构中

  线性探查技术分为两种。第一种是软删除方法。我们使用一个特殊的值（标记）来表示键值对被删除了（惰性删除或软删除），而不是真的删除它。经过一段时间，散列表被操作过后，我们会得到一个标记了若干删除位置的散列表。这会逐渐降低散列表的效率，因为搜索键值会随时间变得更慢。能快速访问并找到一个键是我们使用散列表的一个重要原因。

  第二种方法需要检验是否有必要将一个或多个元素移动到之前的位置。当搜索一个键的时候，这种方法可以避免找到一个空位置。如果移动元素是必要的，我们就需要在散列表中挪动键值对。

• 双散列

二叉树

Binary Search Tree

二叉树中的节点最多只能有两个子节点：一个是左侧子节点，另一个是右侧子节点。这个定义有助于我们写出更高效地在树中插入、查找和删除节点的算法。二叉树在计算机科学中的应用非常广泛。

二叉搜索树（BST）是二叉树的一种，但是只允许你在左侧节点存储（比父节点）小的值，在右侧节点存储（比父节点）大的值。

insert

insertNode(node, key) {
  if (this.compareFn(key, node.key) === Compare.LESS_THAN) {
    if (node.left == null) { // 比当前节点小，放左边
      node.left = new Node(key);
    } else {
      this.insertNode(node.left, key);
    }
  } else {
    if (node.right == null) { // 比当前节点大，放右边
      node.right = new Node(key);
    } else {
      this.insertNode(node.right, key); 
    }
  }
}

二叉树的遍历

二叉树的遍历

• 前序遍历：若二叉树为空，则空操作返回，否则先访问根结点，然后前序遍历左子树，再前序遍历右子树。
• 中序遍历：若树为空，则空操作返回，否则从根结点开始（注意并不是先访问根结点)，中序遍历根结点的左子树，然后访问根结点，最后中序遍历右子树。
• 后序遍历：若树为空，则空操作返回，否则从左到右先叶子后结点的方式遍历访问左右子树，最后访问根结点。

从尾到头打印链表

1. 先给递归算法的基线条件
2. 然后调用自身即递归
3. 最后再操作当前节点 （后序遍历）

var reversePrint = function(head) {
  if (!head) return []
  const result = reversePrint(head.next)
  result.push(head.val)
  return result
};

AVL与红黑树

• AVL: 一般用平衡因子判断是否平衡并通过旋转来实现平衡，左右子树树高不超过1，和红黑树相比，AVL树是高度平衡的二叉树，平衡条件必须满足（所有节点的左右子树高度差不超过1）。不管我们是执行插入还是删除操作，只要不满足上面的条件，就要通过旋转来保持平衡，而的由于旋转比较耗时，由此我们可以知道AVL树适合用于插入与删除次数比较少，但查找多的情况
• 红黑树：也是一种平衡二叉树，但每个节点有一个存储位表示节点的颜色，可以是红或黑。通过对任何一条从根到叶子的路径上各个节点着色的方式的限制，红黑树确保没有一条路径会比其它路径长出两倍，因此，红黑树是一种弱平衡二叉树（由于是弱平衡，可以看到，在相同的节点情况下，AVL树的高度<=红黑树），相对于要求严格的AVL树来说，它的旋转次数少，所以对于搜索，插入，删除操作较多的情况下，用红黑树。

重建二叉树

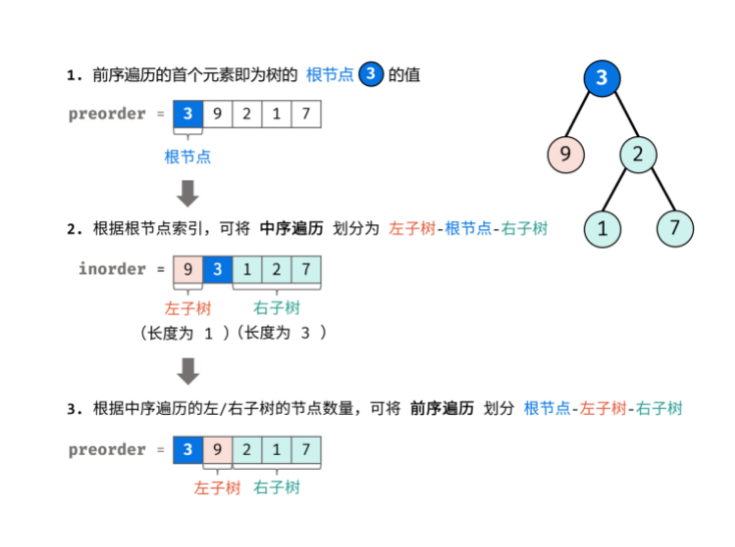
var buildTree = function(preorder, inorder) {
    if(preorder.length === 0) return null;
    const rootVal = preorder[0];
    const rootNode = new TreeNode(rootVal);
    if(preorder.length === 1 ) return rootNode; 
    const index = inorder.indexOf(rootVal);
    rootNode.left = buildTree(preorder.slice(1, index+1), inorder.slice(0, index));
    rootNode.right = buildTree(preorder.slice(index+1), inorder.slice(index+1));
    return rootNode;
};

二叉堆与堆排序

堆

• 堆是一个完全二叉树。
• 完全二叉树： 二叉树除开最后一层，其他层结点数都达到最大，最后一层的所有结点都集中在左边（左边结点排列满的情况下，右边才能缺失结点）。
• 大顶堆：根结点为最大值，每个结点的值大于或等于其孩子结点的值。
• 小顶堆：根结点为最小值，每个结点的值小于或等于其孩子结点的值。
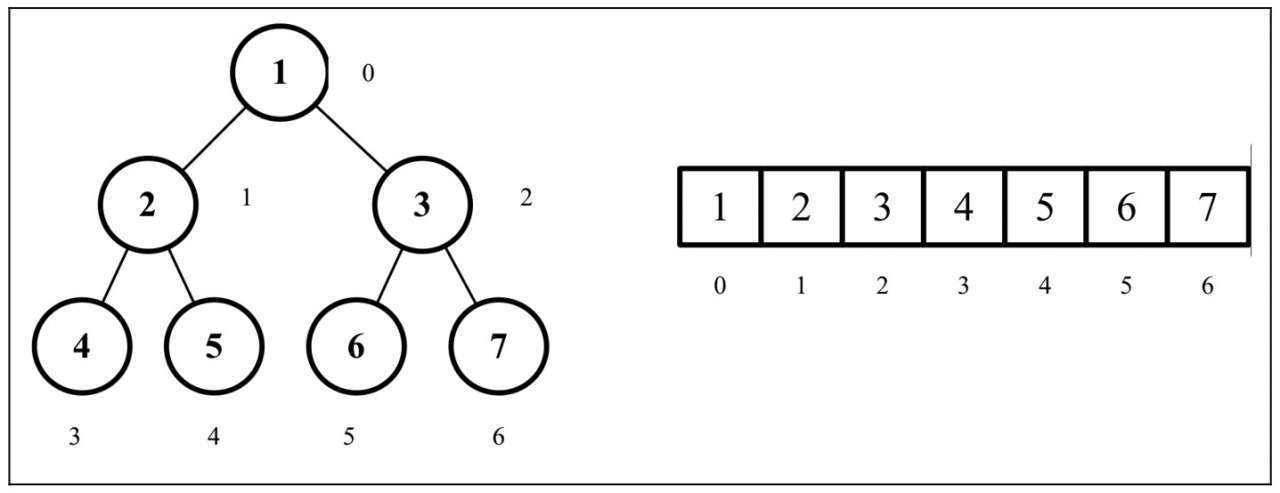
• 堆的存储： 堆由数组来实现，相当于对二叉树做层序遍历。

二叉堆

二叉堆是一种特俗的二叉树，二叉堆是计算机科学中一种非常著名的数据结构，由于它能高效、快速地找出最大值和最小值，常被应用于优先队列。它也被用于著名的堆排序算法中。

• 它是一棵完全二叉树，表示树的每一层都有左侧和右侧子节点（除了最后一层的叶节点），并且最后一层的叶节点尽可能都是左侧子节点，这叫作结构特性。
• 二叉堆不是最小堆 MinHeap就是最大堆 MaxHeap。最小堆允许你快速导出树的最小值，最大堆允许你快速导出树的最大值。所有的节点都大于等于（最大堆）或小于等于（最小堆）每个它的子节点。这叫作堆特性。

堆排序

二叉树做升序排序，总共分为三步：

1. 将初始二叉树转化为大顶堆（heapify）（实质是从第一个非叶子结点开始，从下至上，从右至左，对每一个非叶子结点做shiftDown操作），此时根结点为最大值，将其与最后一个结点交换。
2. 除开最后一个结点，将其余节点组成的新堆转化为大顶堆（实质上是对根节点做shiftDown操作），此时根结点为次最大值，将其与最后一个结点交换。
3. 重复步骤2，直到堆中元素个数为1（或其对应数组的长度为1），排序完成。

// 交换两个节点
function swap(A, i, j) {
  let temp = A[i];
  A[i] = A[j];
  A[j] = temp; 
}

// 将 i 结点以下的堆整理为大顶堆，注意这一步实现的基础实际上是：
// 假设 结点 i 以下的子堆已经是一个大顶堆，shiftDown函数实现的
// 功能是实际上是：找到 结点 i 在包括结点 i 的堆中的正确位置。后面
// 将写一个 for 循环，从第一个非叶子结点开始，对每一个非叶子结点
// 都执行 shiftDown操作，所以就满足了结点 i 以下的子堆已经是一大
//顶堆
function shiftDown(A, i, length) {
  let temp = A[i]; // 当前父节点
// j<length 的目的是对结点 i 以下的结点全部做顺序调整
  for(let j = 2*i+1; j<length; j = 2*j+1) {
    temp = A[i];  // 将 A[i] 取出，整个过程相当于找到 A[i] 应处于的位置
    if(j+1 < length && A[j] < A[j+1]) { 
      j++;   // 找到两个孩子中较大的一个，再与父节点比较
    }
    if(temp < A[j]) {
      swap(A, i, j) // 如果父节点小于子节点:交换；否则跳出
      i = j;  // 交换后，temp 的下标变为 j
    } else {
      break;
    }
  }
}

// 堆排序
function heapSort(A) {
  // 初始化大顶堆，从第一个非叶子结点开始
  for(let i = Math.floor(A.length/2-1); i>=0; i--) {
    shiftDown(A, i, A.length);
  }
  // 排序，每一次for循环找出一个当前最大值，数组长度减一
  for(let i = Math.floor(A.length-1); i>0; i--) {
    swap(A, 0, i); // 根节点与最后一个节点交换
    shiftDown(A, 0, i); // 从根节点开始调整，并且最后一个结点已经为当
                         // 前最大值，不需要再参与比较，所以第三个参数
                         // 为 i，即比较到最后一个结点前一个即可
  }
}

let Arr = [4, 6, 8, 5, 9, 1, 2, 5, 3, 2];
heapSort(Arr);
alert(Arr);

复杂度分析：adjustHeap 函数中相当于堆的每一层只遍历一个结点，因为 具有n个结点的完全二叉树的深度为[log2n]+1，所以 shiftDown的复杂度为 O(logn)，而外层循环共有 f(n) 次，所以最终的复杂度为 O(nlogn)。

DFS与BFS

📗 深度优先遍历（Depth First Search, 简称 DFS） 与广度优先遍历（Breath First Search）是图论中两种非常重要的算法，生产上广泛用于拓扑排序，寻路（走迷宫），搜索引擎，爬虫等。

深度优先遍历

深度优先遍历主要思路是从图中一个未访问的顶点 V 开始，沿着一条路一直走到底，然后从这条路尽头的节点回退到上一个节点，再从另一条路开始走到底...，不断递归重复此过程，直到所有的顶点都遍历完成。

这就是树的前序遍历,实际上不管是前序遍历，还是中序遍历，亦或是后序遍历，都属于深度优先遍历。

1、递归实现

preOrderTraverse(callback) {
  this.preOrderTraverseNode(this.root, callback);
}

preOrderTraverseNode(node, callback) {
  if (node ! = null) {
    callback(node.key);
    this.preOrderTraverseNode(node.left, callback);
    this.preOrderTraverseNode(node.right, callback);
  }
}

2、遍历实现

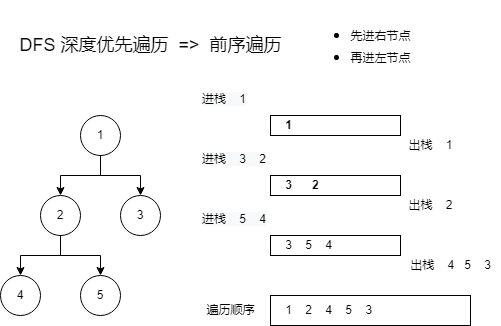
public static void dfsWithStack(Node root) {
    if (root == null) {
        return;
    }

    Stack<Node> stack = new Stack<>();
    // 先把根节点压栈
    stack.push(root);
    while (!stack.isEmpty()) {
        Node treeNode = stack.pop();
        // 遍历节点
        process(treeNode)

        // 先压右节点
        if (treeNode.right != null) {
            stack.push(treeNode.right);
        }

        // 再压左节点
        if (treeNode.left != null) {
            stack.push(treeNode.left);
        }
    }
}

广度优先遍历

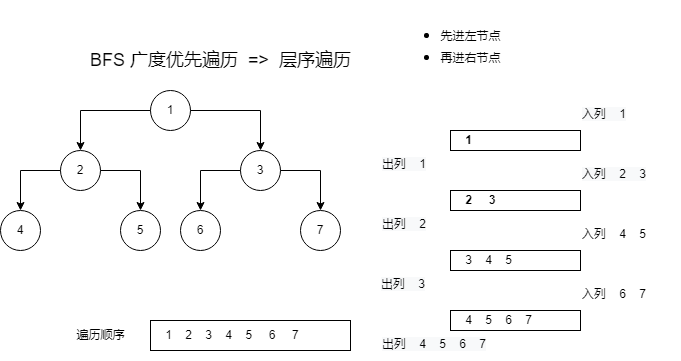
private static void bfs(Node root) {
    if (root == null) {
        return;
    }
    Queue<Node> stack = new LinkedList<>();
    stack.add(root);

    while (!stack.isEmpty()) {
        Node node = stack.poll();
        System.out.println("value = " + node.value);
        Node left = node.left;
        if (left != null) {
            stack.add(left);
        }
        Node right = node.right;
        if (right != null) {
            stack.add(right);
        }
    }
}

动态规划

📗 动态规划跟带备忘录的递归解法基本思想是一致的，都是减少重复计算，时间复杂度也都是差不多。但是呢：

• 带备忘录的递归，是从f(10)往f(1）方向延伸求解的，所以也称为自顶向下的解法。
• 动态规划从较小问题的解，由交叠性质，逐步决策出较大问题的解，它是从f(1)往f(10）方向，往上推求解，所以称为自底向上的解法。

动态规划有几个典型特征，最优子结构、状态转移方程、边界、重叠子问题。在青蛙跳阶或斐波那契数问题中：

• f(n-1)和f(n-2) 称为 f(n) 的最优子结构
• f(n)= f（n-1）+f（n-2）就称为状态转移方程
• f(1) = 1, f(2) = 2 就是边界啦
• 比如f(10)= f(9)+f(8),f(9) = f(8) + f(7) ,f(8)就是重叠子问题。

记忆化递归

const cache = [0, 1]

var fib = function(n) {
    if(cache[n] != null) return cache[n]
    const result = (fib(n-1) + fib(n-2)) % 1000000007; 
    if(cache[n] == null) cache[n] = result
    return cache[n]
};

动态规划

var fib = function(n) {
    if(n === 0) return 0; // 边界
    if(n === 1) return 1;
    let a = 1, b = 0; // 最优子结构 f(n-1)和f(n-2)
    let result = 0;
    for(let i = 2; i <= n; i++) {
        result = (a+b) % 1000000007; // 状态转移方程 f(n)= f（n-1）+f（n-2）
        b = a;
        a = result
    }
    return result
};

排序和搜索算法

冒泡排序

冒泡排序

• 冒泡排序是比较相邻的两个项，如果第一个比第二个大，则交换它们。
• 元素项向上移动至正确的顺序，就好像气泡升至表面一样，冒泡排序因此而得名。
• 冒泡排序可能是所有排序算法中最简单的，但从运行时间的角度而言，冒泡排序是最差的一个。

function toggleItem(array, index1, index2) {
    [array[index1], array[index2]] = [array[index2], array[index1]];
}
function bubbleSort(arr) {
    const { length } = arr
    for (let i = 0; i < length; i++) {
        // 每一次外循环之后，都能确定一个最大值
        for (let j = 0; j < length - 1 - i; j++) {
            // 每次内循环，间隔对比找到最大的值，放到后面
            // 如果前者比后者大，调换位置达到从小到大的效果
            if (arr[j] > arr[j + 1]) toggleItem(arr, j, j + 1)
        }
    }
    return arr
}

选择排序

选择排序

• 选择排序算法是一种原址比较排序算法。
• 选择排序大致的思路是找到数据结构中的最小值并将其放置在第一位，接着找到第二小的值将其放在第二位，以此类推。

function selectSort(arr) {
    const { length } = arr
    let minIndex;
    for (let i = 0; i < length; i++) {
        minIndex = i;
        // 每次内循环，遍历对比找到最小值的索引，所以每次都能确定一个最小值
        for (let j = i + 1; j < length; j++) {
            if (arr[j] < arr[minIndex]) {
                minIndex = j
            }
        }
        // 如果找到比当前开始数值更小的索引，交换位置
        if (minIndex !== i) {
            toggleItem(arr, i, minIndex)
        }
    }
    return arr
}

插入排序

如果要将[1,2,3,0]数组当中的0移动到第一个位置，我们需要设置一个变量temp保存arr[3]；

然后从右向左遍历将所有数组项的索引右移一位，最后把0temp赋值给arr[0]`即可。

const arr = [1,2,3,0];
let i = arr.length - 1;
let temp = arr[i];  // 0
while(i>0) {
    arr[i] = arr[i-1];
    i--;
}
arr[0] = temp;
console.log(arr);  // [0, 1, 2, 3]

插入排序每次排一个数组项，以此方式构建最后的排序数组。

function insertSort(array) {
    const {
        length
    } = array
    let temp;

    for (let i = 1; i < length; i++) {
        let j = i;
        temp = array[j];
        while (j > 0 && array[j - 1] > temp) {
            array[j] = array[j - 1]
            j--;
        }
        array[j] = temp;
    }
    return array;
}

注意：在排序小型数组时，此算法比选择排序和冒泡排序性能要好

归并排序

📗 归并排序是第一个可以实际使用的排序算法，我们之前的三种算法性能不是特别的好，但归并排序性能不错，在JavaScript中，Array.prototype.sort()方法，ECMAScript并没有定义使用哪种排序算法，而是交给浏览器厂商自己去实现，而对于谷歌V8引擎，其使用了快速排序的变体；在Firefox浏览器中，则是使用了归并排序。

实现

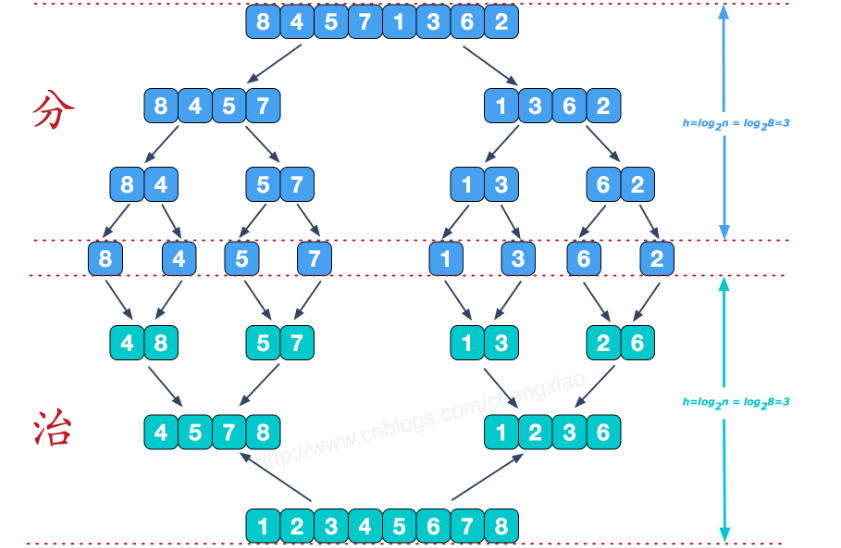
首先，假设我们有两个已经是排序过的数组，实现一个将这两个数组合并成一个的merge方法:

function merge(left, right) {
    let i = 0;
    let j = 0;
    // 需要一个额外的数组空间保存结果
    const result = [];
    // 当left和right都还有未遍历项时
    while (i < left.length && j < right.length) {
        // 找到left和right当中的最小一项push到result,然后索引自增1
        result.push(left[i] > right[j] ? right[j++] : left[i++]);
    }
    // left如果已经遍历完, 将right连接到result,反之将left的剩余项连接到result
    // result.concat(i < left.length ? left.slice(i) : right.slice(j))
    return result.concat(i == left.length ? right.slice(j) : left.slice(i))
    
}

console.log(merge([1, 2], [0, 4]));  // [0, 1, 2, 4]
console.log(merge([2, 3, 5], [0, 4]));  // [0, 2, 3, 4, 5]
console.log(merge([1], [0]));  // [0, 1] 

归并排序是一种分而治之的算法，其思想是将原始数组切分为较小的数组，直到每个小数组只有一个位置，接着将小数组归并成较大的数组，直到最后只有一个排序完毕的大数组。

function mergeSort(array) {
    if (array.length > 1) {
        const { length } = array
        const middle = Math.floor(length / 2)
        const left = mergeSort(array.slice(0, middle))
        const right = mergeSort(array.slice(middle, length))
        array = merge(left, right)
    }
    return array
}

const result = mergeSort([8, 7, 6, 5, 4, 3, 2, 1])
console.log(result) // [1, 2, 3, 4, 5, 6, 7, 8]

总结

• 归并排序是稳定排序，它也是一种十分高效的排序，能利用完全二叉树特性的排序一般性能都不会太差。从上文的图中可看出，每次合并操作的平均时间复杂度为O(n)，而完全二叉树的深度为|log2n|。总的平均时间复杂度为O(nlogn)。而且，归并排序的最好，最坏，平均时间复杂度均为O(nlogn)。
• 归并的空间复杂度就是那个临时的数组和递归时压入栈的数据占用的空间：n + logn；所以空间复杂度为: O(n)

快速排序

📗 快速排序也许是最常用的排序算法了。它的复杂度为O(nlog(n))，且性能通常比其他复杂度为O(nlog(n))的排序算法要好。

和归并排序一样，快速排序也使用分而治之的方法，将原始数组分为较小的数组（但它没有像归并排序那样将它们分割开）。

快速排序的思想很简单，整个排序过程只需要三步：

• 在数据集之中，选择一个元素作为"基准"（pivot）。
• 所有小于"基准"的元素，都移到"基准"的左边；所有大于"基准"的元素，都移到"基准"的右边。
• 对"基准"左边和右边的两个子集，不断重复第一步和第二步，直到所有子集只剩下一个元素为止。

基本实现

function quickSort(arr) {
  if(arr.length <= 1) return arr;
  const mid = arr.splice(Math.floor(arr.length/2),1)[0];
  const left = [];
  const right = [];
  for(let i = 0; i < arr.length; i ++) {
    if(arr[i] < mid) {
      left.push(arr[i])
    }else {
      right.push(arr[i])
    }
  }
  return quickSort(left).concat([mid], quickSort(right))
}

🐛 需在原数组当中移除中值，否则递归会栈溢出

[6, 3, 5] 如果不移除中值3，会全push在right，造成死循环

[3, 5] 如果不移除中值5，会全push在left，造成死循环

双指针

使用数组首项作为基准，左指针寻找比基准大的，右指针寻找比基准小的，交换位置

当左右指针重合，即一次遍历完，交换基准

function quickSort(arr, begin, end) {
  if (begin >= end) {
      return
  }
  let temp = arr[begin];
  let left = begin;
  let right = end;
  while(right > left) {
      while(right > left && arr[right] >= temp) {
          right--;
      }
      while(right > left && arr[left] <= temp) {
          left++;
      }
      [arr[left], arr[right]] = [arr[right], arr[left]];
  }

  [arr[begin], arr[right]] = [arr[right], arr[begin]];
  quickSort(arr, begin, right - 1);
  quickSort(arr, right + 1, end);
  return arr;
}
const arr = [3, 6, 1, 2, 5, 4];
const result = quickSort(arr, 0, arr.length - 1);
console.log(result);

计数排序

📗 计数排序是我们学到的第一个分布式排序，分布式排序使用已组织好的辅助数据结构，然后进行合并，得到排好序的数组。计数排序使用一个用来存储每个元素在原始数组中出现次数的临时数组，在所有元素都计数完完成后，临时数组已排好序并可迭代已构建排序后的结果数组。

计数排序是一种用来排序整数优秀的算法，它的时间复杂度非常简单，但其额外引入了辅助数据结构从而需要更多的内存空间。

function countingSort(array) {
    if (array.length < 2) {
        return array
    }
    const maxValue = findMaxValue(array)
    const counts = new Array(maxValue + 1)
    array.forEach(item => {
        if (!counts[item]) {
            counts[item] = 0
        }
        counts[item]++
    })
    let sortIndex = 0
    counts.forEach((item, index) => {
        while (item > 0) {
            array[sortIndex++] = index
            item--
        }
    })
    return array
}
function findMaxValue(array) {
    let max = array[0]
    for (let index = 1; index < array.length; index++) {
        if (array[index] > max) {
            max = array[index]
        }
    }
    return max
}

const result = countingSort([5, 4, 3, 2, 1])
console.log(result) // [1, 2, 3, 4, 5]

顺序搜索

📗 顺序搜索(线性搜索)是最基本的搜索算法，它的机制是，将每一个数据结构中的元素和我们要找的元素做比较，一直到找到位置。顺序搜索是最低效的一种搜索算法。

function sequentSearch (array, value) {
    let result = -1
    for(let index = 0; index < array.length; index++) {
        if (array[index] === value) {
            result = index
            return
        }
    }
}

二分搜索

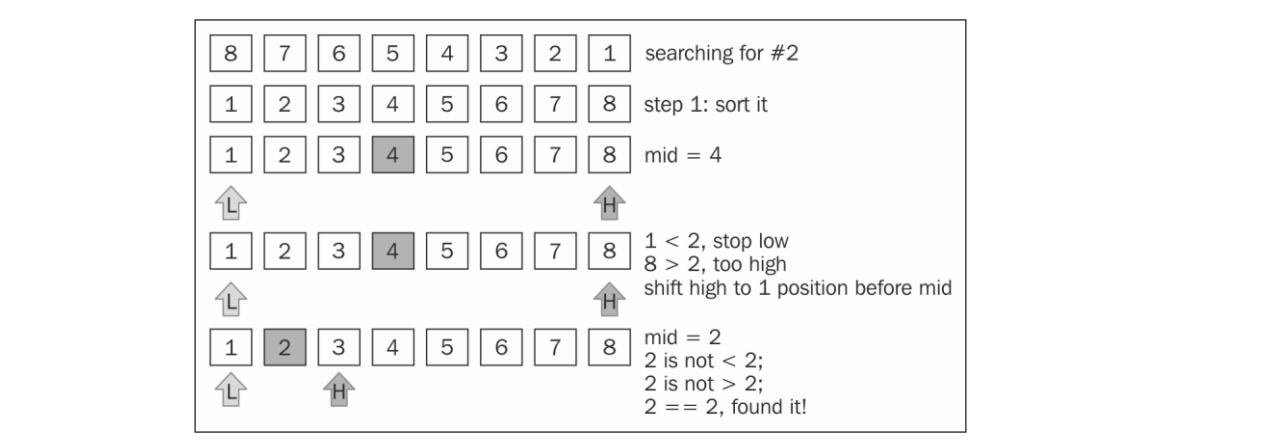
📗 二分搜索算法的原理和猜数字游戏类似，假设有1-100的数，一个人猜，另一个人只需要回答高了还是低了，一直到找到这个数位置。

二分搜索算法对数据结构有一定的要求，它首先要求数据结构已经是排好序的，其次它还要遵守如下的规则：

二分搜索

1. 首先选择数组的中间值。

2. 如果选中的值是待搜索的值，那么停止搜索。

3. 如果待搜索的值比选中的值要小，则返回步骤1并在选中值左边的子数组中查找。

4. 如果待搜索的值比选中的值要大，则返回步骤1并在选中值的右边的子数组中查找。

function binarySearch (array, value) {
    array.sort()
    let low = 0
    let high = array.length - 1
    while (low <= high) {
        const mid = Math.floor((low + high) / 2)
        const element = array[mid]
        if (value === element) {
            return true
        } else if (value < element) {
            high = mid - 1
        } else {
            low = mid + 1
        }
    }
    return false
}
console.log(binarySearch([8, 7, 6, 5, 4, 3, 2, 1], 2))  // true

代码分析：为了进一步简单化，我们使用了内置的Array.prototype.sort()方法来进行排序，也可以使用我们之前学到的任何排序算法来替换。

以下是二分搜索算法的搜索示意图：

内插搜索

🔖 内插搜索（插值查找）是改良版的二分搜索。二分搜索总是基于中间位置上的值为参照物，而内插搜索会选择接近查找的值作为参照物。

即通过一个计算后的比例值获得参照的下标，这个值相比二分搜索的中间值，一般会更接近我们要查找的值，从而减少了搜索的时间。

步骤如下：

1. 选择期望比例 delta = (选择的值-最小值)/(最大值-最小值)
2. 参考下标 position = 最小值 + Math.floort((最大值-最小值) * delta )

const interpolationSearch = (array,value) => {
    const {length} =array
    let low = 0
    let high = length-1
    let position = -1
    let delta = -1
    while(low<high) {
        delta = (value-array[low])/(array[high]-array[low])
        position = low + Math.floor((high - low) * delta);
        if (array[position] === value) {
            return position
        }
        if (array[position] < value) {
            low = position +1
        } else {
            high = position -1
        }
    }
}
console.log(interpolationSearch([1,2,3,4,5,6,7,8,9],6));

内插搜索的高效性只针对均匀分布的数组，而对于分布不均匀的数组，插值查找便不再适用了

随机算法

🔖 将一个数组中的值进行随机排列

function shuffle(array) {
    for (let i = array.length -1; i > 0; i--) {
        const randomIndex = Math.floor(Math.random() * (i + 1));
        swap(array, i, randomIndex);
    }
    return array;
}

日常记录

树的路径

let list1 = [
  {
    "id": "ab",
    "children": [
      {
        "id": "cd",
        "children": [
          {
            "id": "ef",
            "children": []
          }
        ]
      },
      {
        "id": "ce",
        "children": [
          {
            "id": "eg",
            "children": []
          }
        ]
      }
    ]
  }
]

const test = function(data) {
    const initPath = function(node, parentNestPId) {
        if(!parentNestPId) {
            node.nestPId = node.id
        }else {
            node.nestPId = `${parentNestPId}>${node.id}`
        }
        if(node.children && node.children.length) {
            node.children.forEach(i=> initPath(i, node.nestPId))
        }
    }
    data.forEach(m=> {
        initPath(m)
    })
    return data
}

const result = test(list1)

结果：

// [
//     {
//       "id": "ab",
//       "children": [
//         {
//           "id": "cd",
//           "nestPId": "ab>cd",
//           "children": [
//             {
//               "id": "ef",
//               "children": [],
//               "nestPId": "ab>cd>ef"
//             }
//           ],
//         },
//         {
//           "id": "ce",
//           "nestPId": "ab>ce",
//           "children": [
//             {
//               "id": "eg",
//               "children": [],
//               "nestPId": "ab>ce>eg"
//             }
//           ],
//         }
//       ],
//       "nestPId": "ab"
//     }
//   ]